Materi Fisika SMA Potensial Gravitasi Planet

Zsmart.id - Setelah memahami beberapa artikel mengenai konsep dasar gravitasi yakni gaya gravitasi Newton, percepatan yang ditimbulkan oleh gravitasi, medan gravitasi maka selanjutnya kita akan masuk ke topik terakhir mengenai gravitasi yakni potensial gravitasi dengan contoh kasus planet Bumi.

Potensial Gravitasi Bumi

Misalkan sebuah benda yang berada pada titik jauh tak terhingga, ingin dipindahkan ke titik tertentu sejauh r dari pusat planet Bumi maka diperlukan usaha untuk membawa benda tersebut. Besar usaha yang diperlukan yakni : 

\[ W=F.r\]

Jika gaya gravitasi kita masukkan ke persamaan tersebut, maka akan diperoleh :

\[ W=G\frac{Mm}{r}\]

yang merupakan persamaan usaha yang diperlukan untuk memindahkan benda tersebut.

Jika pada persamaan usaha ini kita bagi dengan massa objek tersebut maka akan diperoleh persamaan potensial gravitasi dari planet bermassa M yakni :

\[V=-\frac{W}{r}\]

\[V=-G\frac{M}{r}\]

terlihat dari persamaan akhir ini bahwa potensial gravitasi planet merupakan besaran skalar sehingga cukup menggunakan aljabar sederhana apabila ingin menyelesaikan kasus-kasus mengenai potensial gravitasi.

Selanjutnya, kita akan menyelidiki penerapan konsep potensial gravitasi untuk beberapa kasus-kasus sederhana.

Potensial Gravitasi Pada Bola Pejal

Pada kasus bola pejal (sebuah bola distribusi massanya sama) dapat diidentikkan dengan suatu partikel titik bermassa. Pada bagian ini akan dibagi menjadi tiga titik tinjauan yakni di luar bola, di permukaan bola dan di dalam bola pejal yang berjejari R.

Di luar bola pejal, memenuhi persamaan :

\[V=-G\frac{M}{r}\]

Di permukaan bola pejal, memenuhi persamaan :

\[V=-G\frac{M}{R}\]

Di dalam bola pejal memenuhi persamaan :

\[V=-G\frac{M}{R^{3}}\left(1.5R^{2}-0.5r^{2}\right)\]

dari persamaan tersebut r merupakan jarak benda dari pusat bola pejal. Terlihat bahwa pada pusat planet di mana r = 0, besar potensialnya tidaklah nol, melainkan sebesar 1.5kali potensial di permukaan bola pejal tersebut.

Potensial Gravitasi Pada Bola Berongga

Kasus selanjutnya adalah bagaimana potensial gravitasi dari suatu bola berongga. Sama halnya dengan bola pejal, untuk kasus bola berongga juga akan ditinjau pada tiga titik yakni potensial gravitasi di luar permukaan, di permukaan dan di dalam bola berongga berjejari R.

Di luar bola berongga, memenuhi persamaan :

\[V=-G\frac{M}{r}\]

Di permukaan bola berongga, memenuhi persamaan :

\[V=-G\frac{M}{R}\]

Di dalam bola berongga, memenuhi persamaan :

\[V=-G\frac{M}{R}\]

terlihat potensial gravitasi di dalam bola berongga yakni tetap sebagai konsekuensi dari konsep Gauss.

Potensial Gravitasi Pada Cincin

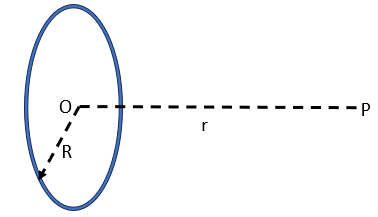
Untuk kasus terakhir yakni bagaimana potensial gravitasi yang dirasakan oleh titik P akibat adanya benda berbentuk cincin dengan jejari R.

pada kasus ini, komponen vertikal akan saling meniadakan dan menyisakan komponen horisontal saja. Besar potensial gravitasi pada titik P dapat diketahui sesuai persamaan :

\[V=-G\frac{M}{\sqrt{R^{2}+r^{2}}}\]

Persamaan ini jika dianalisis untuk potensial pada pusat cincin, berarti r = 0 maka akan diperoleh persamaan potensial gravitasi yang besarnya sama dengan potensial gravitasi umum yang hanya bergantung terhadap jejari objeknya saja.

Demikian informasi singkat mengenai penentuan potensial gravitasi dari suatu planet dan beberapa kasus-kasus sederhana. Semoga bermanfaat!

Share :